Binet’s Formula: \(F_{n} = \frac{1}{\sqrt{5}} \left(\left(\frac{1 + \sqrt{5}}{2}\right) ^{n} - \left(\frac{1 - \sqrt{5}}{2}\right)^{n}\right)\)

where \(F_{n}\) is the \(n^{th}\) Fibonacci number (the recursive definition for the Fibonacci numbers is \(F_{n} = F_{n-1} + F_{n-2}\) where \(F_{1} = 1\) and \(F_{2} = 1\). We can also include \(F_{0} = 0\))

Typically, Binet’s formula over \(\mathbb{N}\) gives us \(F_{1} = 1, F_{2} = 1, F_{3} = 2\) …, but what happens when we use Binet’s formula to find the “\(0.5^{th}\) Fibonacci number” or the “\(\pi^{th}\) Fibonacci number” (if they even exist)? Well, if we try to find \(F_{\pi}\), what we end up with is roughly \(2.11702 + 0.04244i\). We end up with complex numbers because trying to find \(F_{n}\) where \(n \not\in \mathbb{N}\) leads to complex outputs. So, let’s take a look at the outputs of Binet’s formula over some continuous, real domain (e.g. \(\left[0, 5\right]\)).

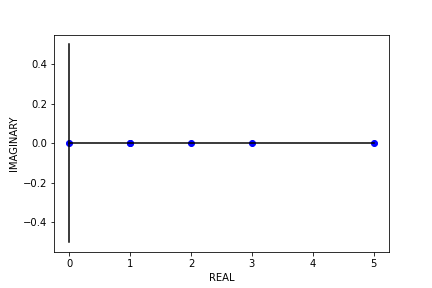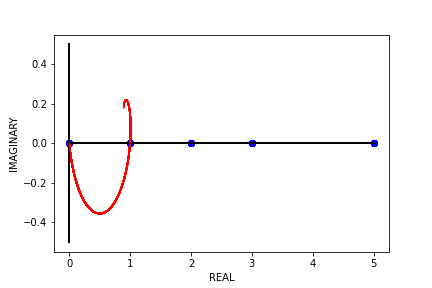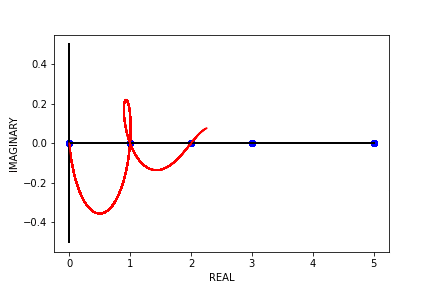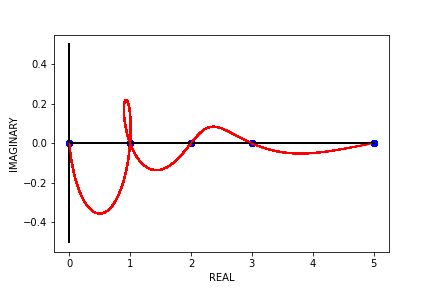
Notice that the only places where Binet’s formula has real outputs on this interval are at the natural numbers, where the outputs are the typical Fibonacci numbers. What about the “negative Fibonacci numbers”? Let’s see what the outputs of Binet’s formula look like on the interval \(\left[-5, 0\right]\).

We end up with \(F_{-1} = 1, F_{-2} = -1, F_{-3} = 2, F_{-4} = -3\) … This large spiral that’s travelling around the complex plane actually intersects the real line at the usual Fibonacci numbers with alternating signs! There is actually a generalization of the typical recurrence relation that allows us to have negative values for \(n\):

\[F_{-n} = \left(-1\right)^{n+1}F_{n}\]

Extending discrete mathematical structures, such as the Fibonacci sequence, to have continuous properties often leads to interesting results. In this example, we saw how Binet’s formula allows us to find complex and negative “Fibonacci numbers”. The field of math that seeks to solve discrete problems about integers using tools from analysis is known as analytic number theory, and it has provided number theorists with other interesting results, such as bounds for the prime counting function and solutions to Diophantine equations.